América Latina: estabilidad macro-financiera y riesgos latentes en un contexto global incierto

Autores¹:

Christian Alcarraz, FLAR, Bogotá, Colombia. – calcarraz@flar.net
Carlos Giraldo, FLAR, Bogotá, Colombia. – cgiraldo@flar.net
Andrea Villarreal, FLAR, Bogotá, Colombia. – avillarreal@flar.net
Liz Villegas , FLAR, Bogotá, Colombia. – lvillegas@flar.net

¹ Las opiniones y visiones son responsabilidad de los autores. No corresponden o necesariamente reflejan la opinión del FLAR ni de sus órganos administrativos.

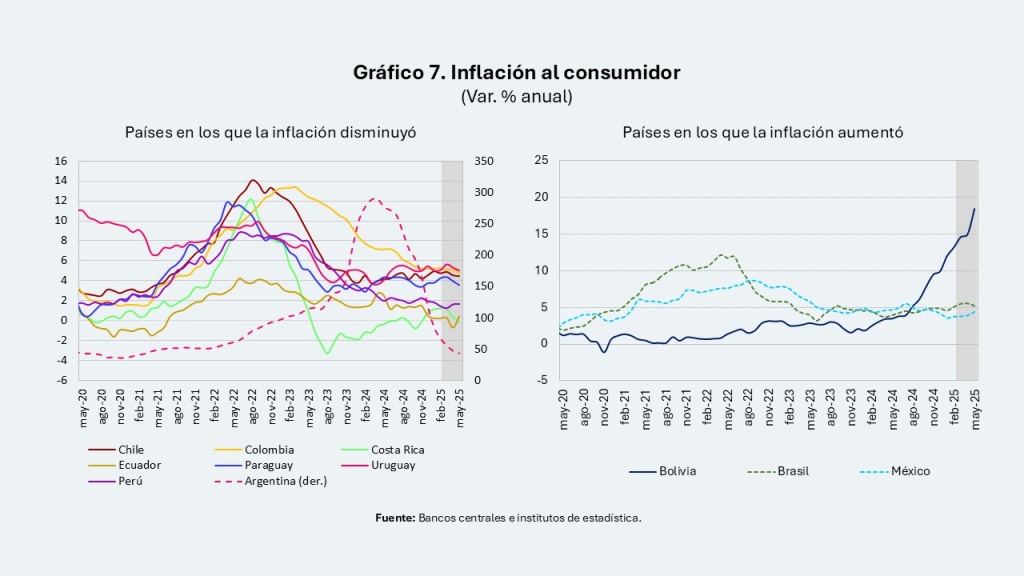
En la primera parte del año, la mayor parte de las economías de la región ha mostrado resiliencia, a pesar de un entorno internacional altamente incierto, caracterizado por la caída de la mayoría de los precios de los commodities y el aumento de los riesgos geopolíticos y comerciales. Varias economías han presentado un descenso del crecimiento del PIB y una continuidad en el proceso de desinflación, con diferencias significativas entre países. En este contexto, los flujos de financiamiento externo hacia la región se han mantenido.

Hacia adelante, los países enfrentan riesgos económicos diferenciados, determinados por un entorno global altamente incierto, y por las distintas capacidades de respuesta monetaria y fiscal.

Choques externos recientes: incertidumbre, precios de materias primas y flujos de financiamiento

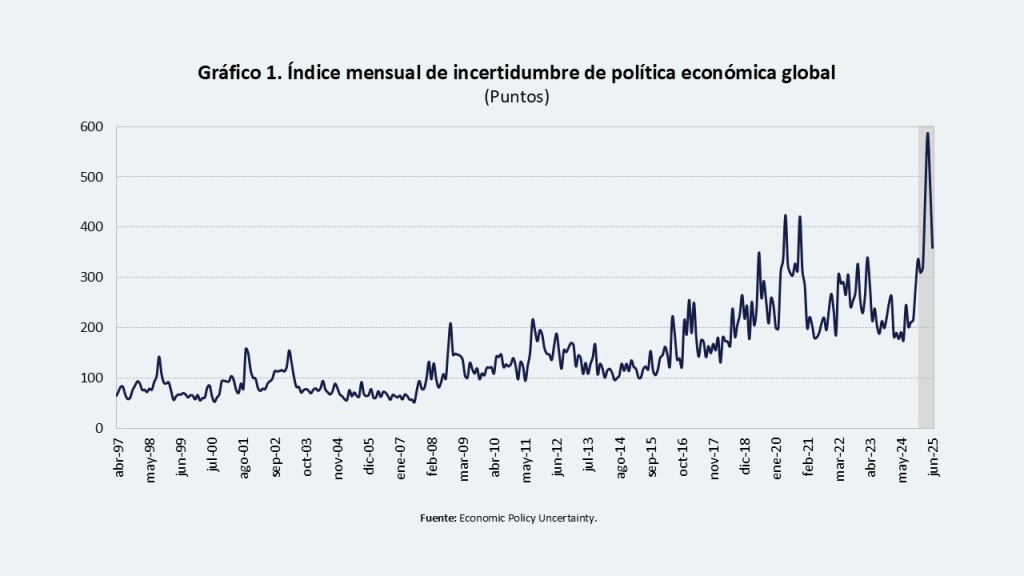
La incertidumbre de la política económica global ha incrementado a niveles históricos debido a las crecientes tensiones comerciales (Gráfico 1). Aunque el pico de incertidumbre se registró tras el anuncio de medidas arancelarias generalizadas por parte del gobierno de Donald Trump (Liberation Day), su posterior disminución ha sido lenta, manteniéndose aún en niveles elevados respecto a 2024.

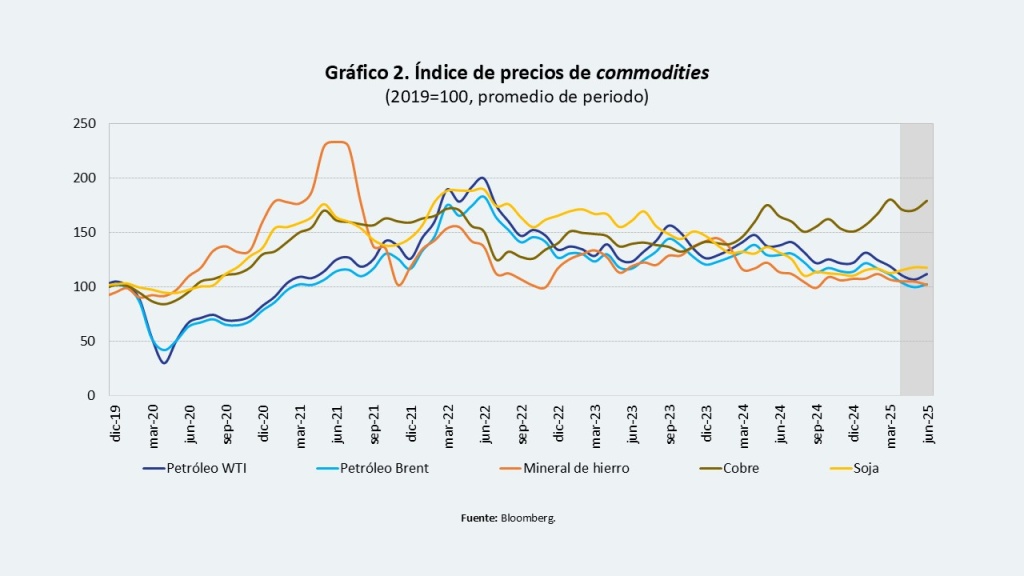
Los precios de los principales productos de exportación de la región han caído, salvo el cobre (Gráfico 2). Su aumento podría explicarse por los anuncios arancelarios del gobierno de Estados Unidos, que habrían generado una anticipación del costo futuro en los precios actuales o una prima de riesgo ante la incertidumbre sobre su implementación.

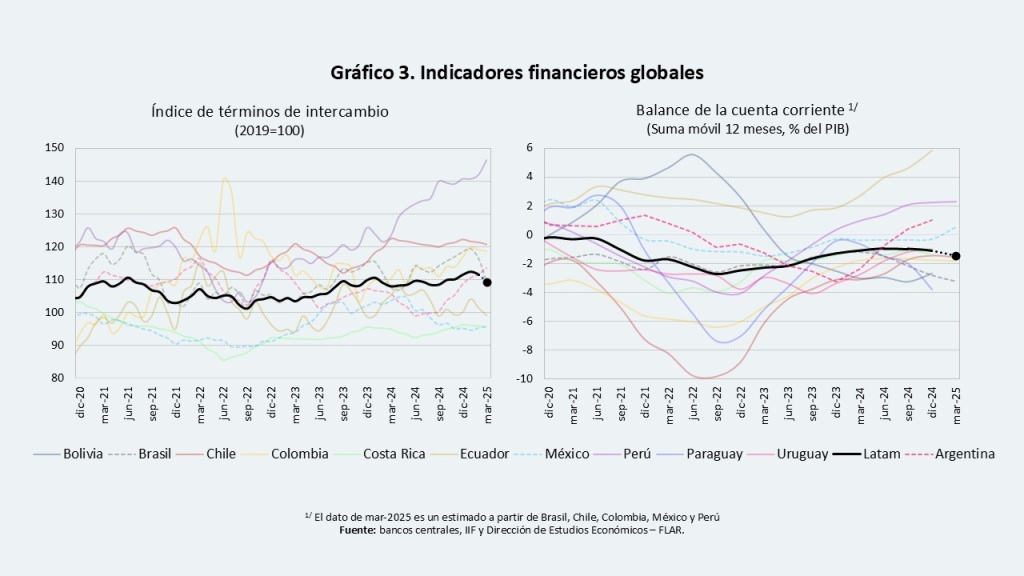
Como consecuencia, los términos de intercambio de la mayoría de los países de América Latina se deterioraron, presionando un leve aumento del déficit en cuenta corriente de gran parte de los países exportadores de commodities durante los primeros meses del año (Gráfico 3).

En el actual contexto global, las cifras preliminares de balanza de pagos del primer trimestre de 2025 sugieren que los flujos de capital hacia América Latina se han mantenido relativamente estables —e incluso habrían aumentado como porcentaje del PIB en varias economías de la región.

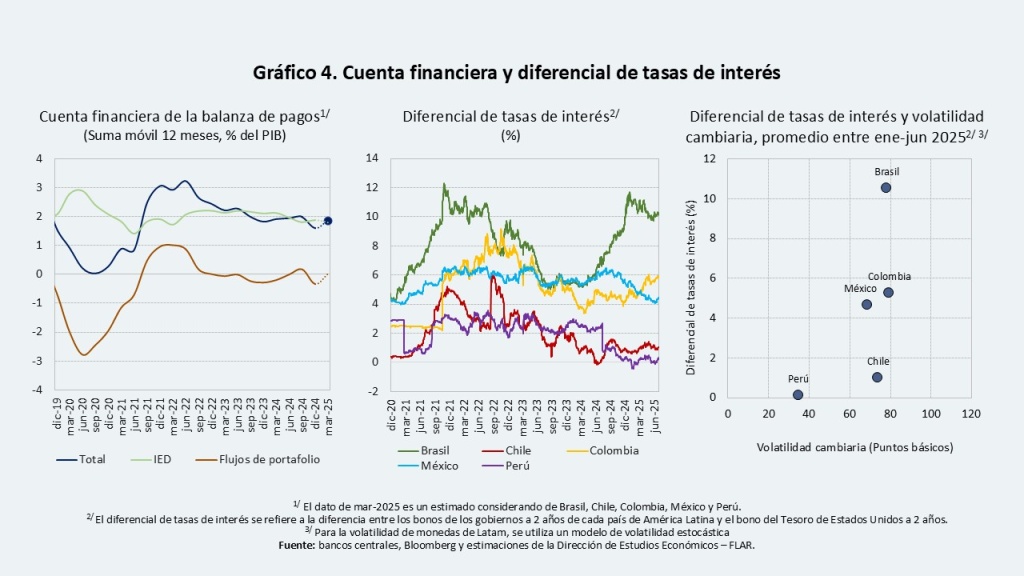
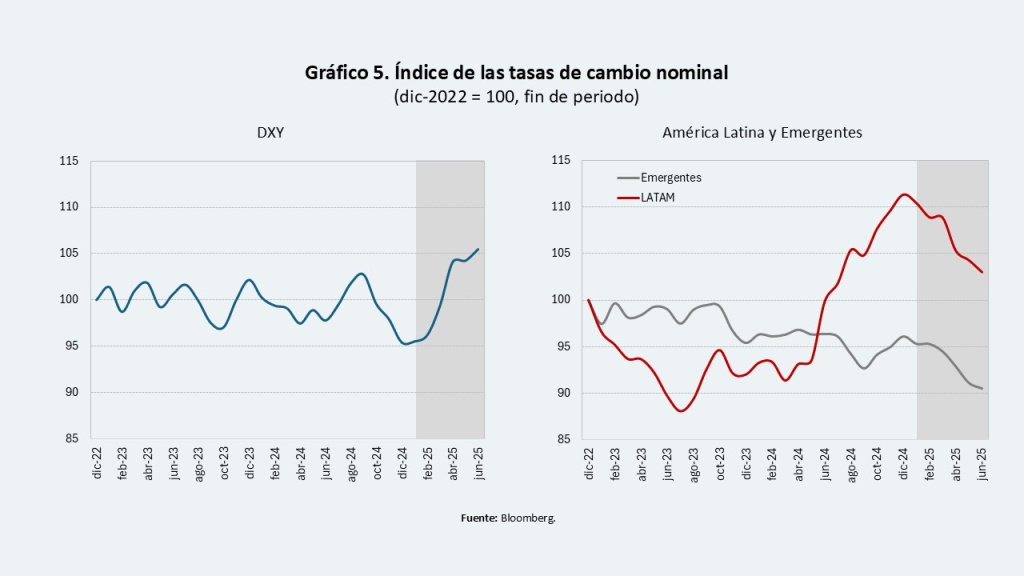
El ingreso de capitales ha estado liderado por los flujos de portafolio, lo que podría deberse, por un lado, a que el diferencial de tasas de interés frente a las inversiones en dólares sigue siendo atractivo para operaciones de carry trade, especialmente en países como Brasil y Colombia (Gráfico 4). Por otro lado, el hecho de que Estados Unidos se haya convertido en el epicentro de la incertidumbre global —por la guerra comercial y los crecientes desequilibrios fiscales— ha debilitado al dólar y motivado decisiones de diversificación por parte de los inversionistas hacia mercados emergentes, incluyendo los de América Latina. Esto ha impulsado la apreciación de la mayoría de las monedas de la región (Gráfico 5).

Crecimiento afectado por factores externos e internos, proceso gradual de desinflación y acciones de política monetaria mixtas

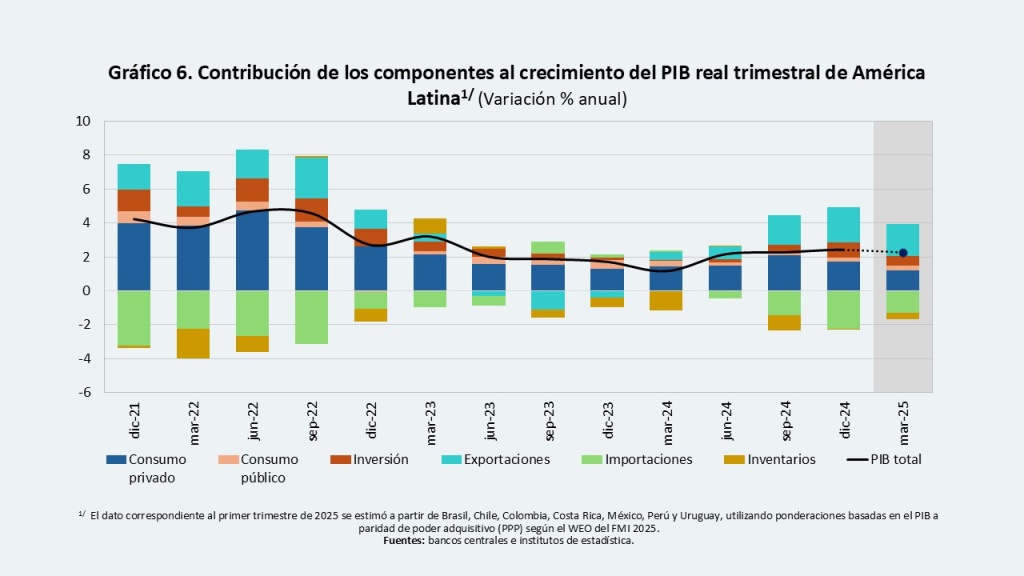
En lo corrido del año, las cifras preliminares del sector real indican un menor crecimiento del PIB frente al cierre del año anterior para la mayor parte de países. Esto como resultado tanto de factores externos como internos (Gráfico 6). El volumen de exportaciones se redujo en línea con la menor demanda externa y la caída de los términos de intercambio, mientras que el consumo de los hogares y la inversión privada se han visto afectados por factores diferenciados entre países, entre los que se encuentran incertidumbre económica o política local, confianza del consumidor o inversionista, alto endeudamiento de los hogares, menor ejecución de inversión pública y altas tasas de interés.

En este contexto, tanto la inflación general como la subyacente han mostrado un descenso gradual en la mayoría de los países (Gráfico 7), con excepción de economías como la de Bolivia, y en menor medida México y Brasil. Por su parte, las decisiones de política monetaria han sido heterogéneas entre los bancos centrales. Mientras Brasil y Uruguay han continuado elevando sus tasas de interés, otros como Chile, Costa Rica y Perú optaron por mantenerlas inalteradas.

Altos niveles de deuda pública y presión sobre los balances fiscales

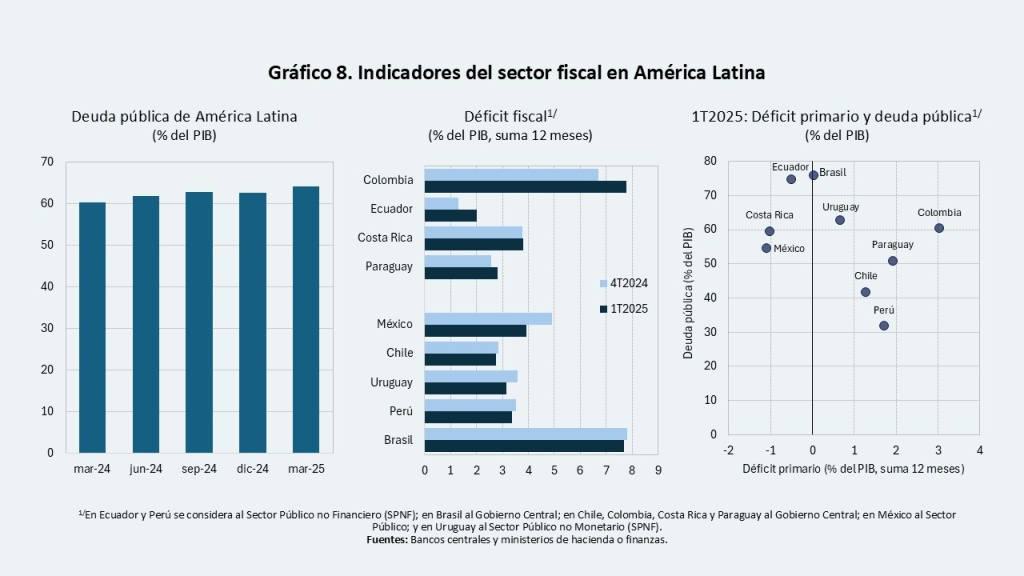
La situación fiscal es heterogénea entre los países de la región, pero preocupa en diversas economías debido a los altos y crecientes niveles de deuda pública como proporción del PIB (Gráfico 8). Los déficits fiscales no son lo suficientemente bajos para estabilizar o reducir dicha proporción. Esta dinámica se explica tanto por un aumento del gasto primario como por un mayor pago de intereses, cuya magnitud varía según el país.

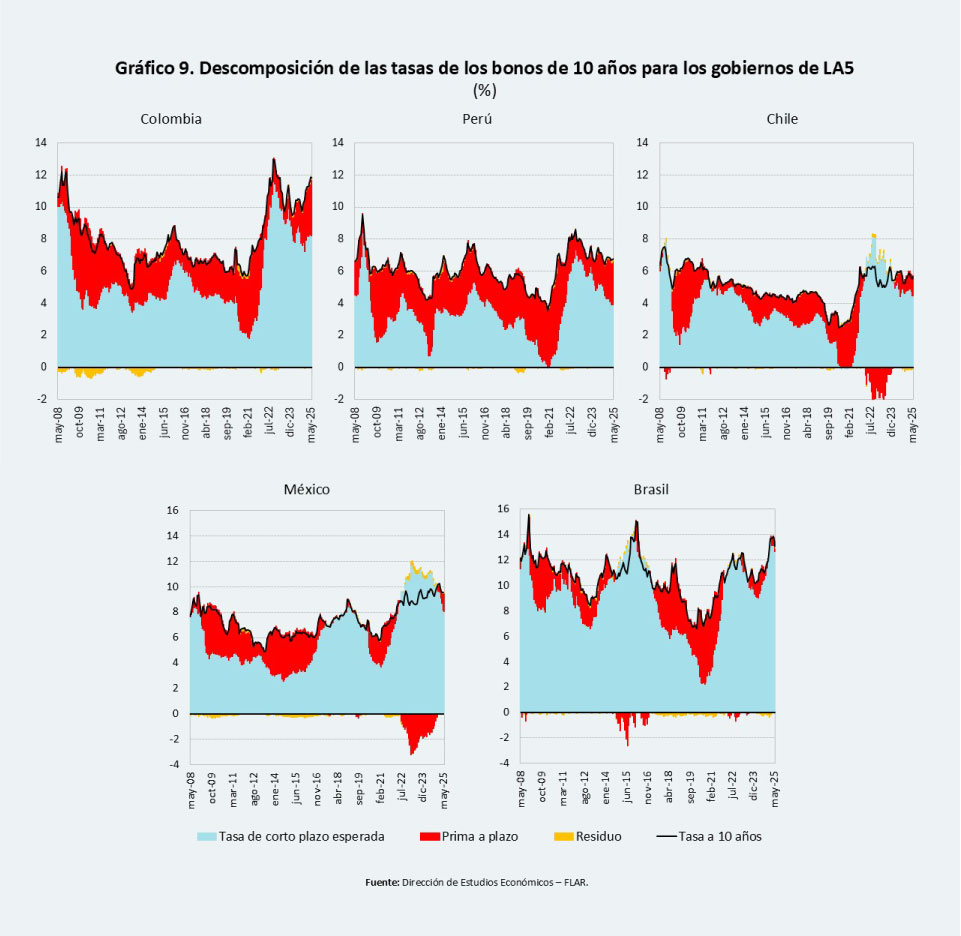
Dada la relevancia del costo de financiamiento soberano y su impacto sobre la trayectoria fiscal, analizamos la estructura de dicho costo para cinco economías de la región con información de su mercado de deuda pública a lo largo de la curva de rendimientos. Para ello, se empleó el modelo ACM (Adrian, Crump y Moench, 2013), que permite descomponer las tasas de interés de largo plazo en dos componentes: (i) el promedio esperado de la tasa de corto plazo y (ii) la prima a plazo (term premium). El primer componente refleja la trayectoria esperada de las tasas de corto plazo, mientras que el segundo incorpora diversos factores de riesgo, como el déficit fiscal, la prima a plazo de EE.UU. y la volatilidad cambiaria (ver recuadro metodológico).

Los resultados obtenidos muestran que la prima a plazo está jugando un papel importante en las tasas de largo plazo en países como Colombia, Perú y Chile, y en menor medida en México y Brasil (Gráfico 9). En este último caso, las tasas de corto plazo explican la mayor parte del comportamiento de las tasas de largo plazo.

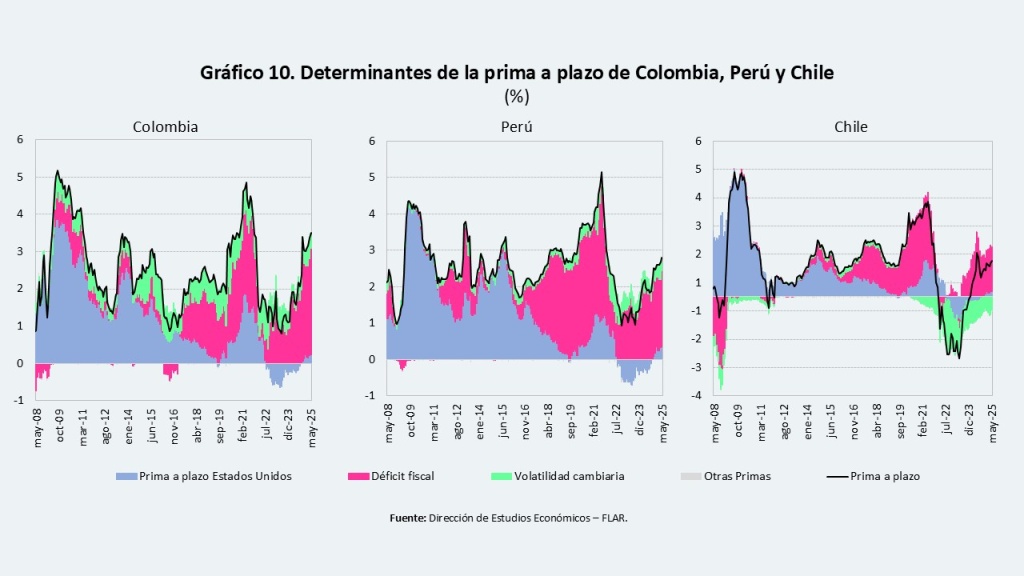
Asimismo, se estimaron los determinantes de la prima a plazo para Colombia, Perú y Chile (recuadro metodológico). Los resultados indican que el déficit fiscal es el factor que más incide en su evolución, especialmente en el caso de Colombia (Gráfico 10).

Perspectivas y riesgos de corto plazo

En lo que resta del año, América Latina seguiría enfrentando un entorno externo e interno desafiante, en línea con las tendencias observadas hasta ahora.

En el frente externo, se anticiparía un crecimiento del PIB en Estados Unidos y China inferior al previsto a comienzos del año. Asimismo, se esperaría que la inflación en Estados Unidos sea persistente, a diferencia de la Eurozona y China, donde la debilidad de la demanda interna ha favorecido su moderación. En el caso estadounidense, las expectativas inflacionarias aún siguen por encima de la meta de la Reserva Federal (Fed).

En este escenario, se prevería que la Fed mantenga su tasa de política monetaria en los niveles actuales. Esto implicaría costos de financiamiento externos aún altos para América Latina (ver FlarBlog: “La evolución económica de Estados Unidos en el primer trimestre de 2025 y el costo de financiamiento externo de América Latina).

Asimismo, se esperaría una caída generalizada de los precios de las materias primas relevantes para los exportadores de estos productos en la región. Esto como resultado de la debilidad de la demanda global y, en ciertos casos, de aumentos en la oferta (por ejemplo, en petróleo y soja).

Al menor dinamismo del sector externo, se sumarían factores vinculados a la demanda interna que tendría como resultado un menor crecimiento de la región. La demanda agregada continuaría débil debido a diversos factores previamente comentados, lo que seguirá afectando el consumo y la inversión privada. En este contexto, se estima que la América Latina —excluyendo a Argentina— crecería un 1,6% en 2025, por debajo del 2,4% registrado en 2024. No obstante, al incluir a Argentina, el crecimiento alcanzaría el 2,0%.

Desde el punto de vista fiscal, se considera probable que el déficit agregado de la región se mantenga en torno al 6% del PIB. Asimismo, se estima que la deuda pública alcance el 62,8% del PIB en 2025, por encima del 60% observado el año anterior.

Finalmente, se identifican diversos riesgos de corto plazo, entre los que destacan: (i) un mayor deterioro fiscal en algunos países, con posibles implicaciones para la estabilidad macroeconómica; (ii) choques externos derivados del agravamiento de tensiones geopolíticas y comerciales; y (iii) una mayor desaceleración de la demanda externa, particularmente en China.

Recuadro metodológico: Estructura de tasa de interés y determinantes de la prima a plazo para LA5

La estructura de la curva de rendimientos proporciona información clave para los bancos centrales. Según Ceballos et al. (2015), la política monetaria convencional influye sobre esta curva y, por consiguiente, sobre las decisiones de financiamiento y gasto de los hogares, empresas y gobierno. En este contexto, la Hipótesis de las Expectativas (HE), formulada por Lutz (1940), sostiene que las tasas de interés de largo plazo reflejan el promedio de las tasas de corto plazo actuales y esperadas.

La Hipótesis de las Expectativas (HE) sostiene que los agentes forman expectativas racionales sobre las tasas de interés, sin errores sistemáticos (Muth, 1961; Cook y Hahn, 1990). Así, las tasas de largo plazo reflejan el promedio esperado de las tasas de corto plazo, y las tasas forward serían estimaciones insesgadas. No obstante, la evidencia empírica sugiere que esta versión simple no explica del todo la dinámica de las tasas largas, lo que ha llevado a incluir una prima por riesgo a plazo variable (Fama y Bliss, 1987; Campbell y Shiller, 1991).

La prima a plazo representa la compensación que exigen los inversionistas por mantener bonos a largo plazo en lugar de renovar sucesivamente bonos de corto plazo. También refleja el riesgo de duración y otros riesgos macro-financieros asociados. Por ello, descomponer las tasas largas en expectativas de tasas cortas y prima a plazo, e identificar los determinantes de esta última, es clave para evaluar cuánto de las tasas de largo plazo responde a expectativas de política monetaria y cuánto a percepciones de riesgo.

Dado que ni las tasas de corto plazo esperadas ni la prima por plazo son observables directamente, se utilizan modelos para estimarlas. Entre los más comunes están los modelos afines de estructura a plazos, calibrados a la curva de rendimientos. El modelo de Adrian, Crump y Moench (2013, en adelante modelo ACM) ofrece una estimación eficiente mediante regresiones lineales. Su simplicidad, junto con resultados comparables a métodos más complejos, ha impulsado su uso. De hecho, la Fed de Nueva York publica regularmente estimaciones de la prima por plazo en Estados Unidos con esta metodología, ampliamente citada en estudios académicos y medios especializados.

Otra aproximación relevante es la de Kim & Wright (2005), que incorpora encuestas de expectativas sobre el rendimiento de letras del Tesoro a tres meses para estimar las tasas de corto plazo esperadas, en lugar de derivarlas de la curva de rendimientos como en el modelo ACM. Sin embargo, debido a la falta de series históricas consistentes de encuestas, este estudio emplea la metodología ACM para cinco economías de la región (Brasil, Chile, Colombia, México y Perú).

Modelo Adrian, Crump & Moench (ACM)

Para estimar las primas a plazo a partir de una curva de rendimientos observada en el mercado se siguen los siguientes procesos.

Curva de Rendimientos Soberano

Sea una curva de rendimientos que contiene tasas equidistantes a lo largo de \(N\) vencimientos. No obstante, en la práctica, en los mercados de deuda, los gobiernos suelen emitir un número de instrumentos menor al número de dichos puntos \((M<N)\), entonces se interpolan \(N\) puntos a partir de \(M\) tasas disponibles en el mercado. Con este propósito, se utiliza un modelo paramétrico de cuatro factores, siguiendo la metodología propuesta por Svensson (1995).

\( y_t^{(n)} = \alpha_0 + \alpha_1 \left[ \frac{1 – e^{-\left( \frac{n}{\lambda_1} \right)}}{\frac{n}{\lambda_1}} \right] + \alpha_2 \left[ \frac{1 – e^{-\left( \frac{n}{\lambda_1} \right)} – e^{-\left( \frac{n}{\bar{\lambda}_1} \right)}}{\frac{n}{\lambda_1}} \right] + \alpha_3 \left[ \frac{1 – e^{-\left( \frac{n}{\lambda_2} \right)} – e^{-\left( \frac{n}{\bar{\lambda}_2} \right)}}{\frac{n}{\lambda_2}} \right] + \eta_t^{(n)} \)

\( n = n_1, n_2, n_3, \ldots, n_M \)

Donde \(y_t^{(n)}\) representa la tasa spot observado en \(t\) con vencimiento a \(n\) periodos \((0<t<n)\). Asimismo, los coeficientes tienen la siguiente interpretación (Svensson, 1995; Diebold y Li, 2006):

\(\alpha_0\): Nivel de la curva de rendimiento, asociado al componente de tasas de largo plazo. Es decir, refleja el nivel al cual converge la curva de rendimientos cuando \(n \to \infty\)
\(\alpha_1\): Captura la sensibilidad de las tasas al factor de corto plazo (pendiente), afectando principalmente los vencimientos cortos.
\(\alpha_2\): Coeficiente vinculado al factor de mediano plazo (primera curvatura), permitiendo el ajuste por convexidad de la curva de rendimiento en vencimientos intermedios.
\(\alpha_3\): Coeficiente asociado al segundo factor de curvatura el cual permite ajustar convexidades adicionales en la curva para vencimientos de muy corto o muy largo plazo, permitiendo flexibilidad para capturar dinámicas complejas en segmentos específicos de la curva.
\(\lambda_1\): Velocidad de decaimiento de la primera curvatura
\(\lambda_2\): Velocidad de decaimiento de la segunda curvatura

Finalmente \(\eta_t^{(\tau)}\) representa el error del modelo

Dado la forma no lineal del modelo utilizaremos Mínimos Cuadrados No Lineales (NLS) en cada periodo \(t\) para estimar los parámetros y a partir de ellos se interpolarán \(N\) tasas distribuidas de forma equidistante a lo largo de los vencimientos considerados \(n = n_1, n_2, n_3,\ldots, n_N\) con el fin de obtener una representación continua, suave y consistente de la curva de rendimientos que facilitara la valorización recursiva de los instrumentos soberanos.

Valorización de bonos bajo no arbitraje

En la literatura de modelos de tasas, se suele asumir una condición de no arbitraje, bajo la cual los instrumentos financieros con las mismas características de riesgo deben tener el mismo precio. Este principio impone restricciones sobre el comovimiento de los rendimientos a distintos plazos y permite la consistencia interna de los precios de mercado.

Los modelos afines gaussianos de estructura temporal de tasas suponen que los rendimientos dependen linealmente de un conjunto de factores de riesgo (de allí el término “afines”), mientras que “gaussianos” se refiere al supuesto de normalidad de dichos factores (Dai y Singleton, 2000; Duffee, 2002; Cochrane y Piazzesi, 2005; Joslin et al., 2011; Adrian et al., 2013). Con base en esta línea de estudios previos, se especifica la siguiente estructura de tasas de interés afín gaussiano.

Sea un vector \(X_t\) de \(K\) factores de riesgo o variables de estado, cuya dinámica bajo la medida física \((P)\), esta descrita por un \(VAR(1)\) gaussiano

\( X_{t+1} = \mu + \Phi X_t + v_{t+1} \)

\( v_{t+1} \sim iid\, N(0, \Sigma) \)

Donde, los factores de riesgo subyacente a la curva de rendimientos \(K = 3\) se identifican mediante Componente Principales (PCA) y se denominan: nivel, pendiente y curvatura (Litterman y Sheikman, 1991). El factor nivel representa el promedio de las tasas a lo largo de los vencimientos de la curva de rendimientos, el factor pendiente está asociado al diferencial de los tramos de largo y corto plazo, mientras que la curvatura refleja los movimientos de los tramos intermedios (Diebold et al., 2004). Existen otros trabajos donde en esta ecuación también incorporan variables macroeconómicas como factores de riesgo adicionales. Ang y Piazzesi (2003), Crump et al. (2018), Gurkaynak y Wright (2012) y Wright (2011).

Bajo el supuesto de ausencia de arbitraje (Dybvig y Ross, 1987) existe un Factor de descuento Estocástico \(M_{t+1}\) (Pricing Kernel, en inglés) es posible fijar en \(t\) el precio \(P_t^{(n)}\) de un bono cupón cero con vencimiento a \(n\) periodos. Este factor permite que los precios del modelo sean consistentes con los observados en el mercado, evitando las oportunidades de arbitraje.

\( P_t^{(n)} = E_t \left[ M_{t+1} P_{t+1}^{(n-1)} \right] \)

\( n = n_1, n_2, n_3, \ldots, n_N \)

El factor de descuento \(M_{t+1}\) es una función exponencial afín a los factores de riesgo

\( M_{t+1} = e^{\left( -r_t – \frac{1}{2} \lambda_t’ \lambda_t – \lambda_t’ \Sigma^{-\frac{1}{2}} v_{t+1} \right)} \)

Donde \(r_t\) representa la tasa de corto plazo (o tasa libre de riesgo) con el vencimiento más corto disponible \(r_t = \ln \left( P_t^{(1)} \right)\) el cual es afín o lineal en los factores de riesgo, de manera similar a los modelos estructurales de tasas de interés como el de Vasicek (1977)

\( r_t = \delta_0 + \delta_1′ X_t \)

Donde \(\delta_0\) y \(\delta_1’\) representan los vectores de sensibilidades

Asimismo, siguiendo a Duffee (2002), el market price of risk \((\lambda_t)\) se define como:

\( \lambda_t = \Sigma^{-\frac{1}{2}} \left( \lambda_0 + \lambda_1 X_t \right) \)

Donde \(\lambda_0\) y \(\lambda_1\) representan los vectores de sensibilidades

Una vez que los precios son encontrados, es posible encontrar sus rendimientos asociados \(y_t^{(n)}\) a través de la siguiente relación

\( y_t^{(n)} = -\frac{1}{n} \ln\left(P_t^{(n)}\right) \)

Se definen los rendimientos en exceso a 1 periodo de un bono con vencimiento \(n\) como

\( rx_{t+1}^{(n-1)} = \ln\left(P_{t+1}^{(n-1)}\right) – \ln\left(P_t^{(n)}\right) – r_t \)

Al unir todas las ecuaciones anteriores, Adrian et al. (2013) demuestra la siguiente ecuación fundamental de valorización

\( 1 = E_t \left[ e^{\left( rx_{t+1}^{(n-1)} – \frac{1}{2} \lambda_t’ \lambda_t – \lambda_t’ \Sigma^{-\frac{1}{2}} v_{t+1} \right)} \right] \)

El modelo ACM asume que \(rx_{t+1}^{(n-1)}\) y \(v_{t+1}\) están distribuidos bajo una distribución normal bivariado, por tanto, se cumple que

\( E_t \left[ rx_{t+1}^{(n-1)} \right] = Cov_t \left( rx_{t+1}^{(n-1)}, v_{t+1}’ \Sigma^{-\frac{1}{2}} v_{t+1} \right) – \frac{1}{2} Var_t \left( rx_{t+1}^{(n-1)} \right) \)

Para simplificar, se denota la siguiente variable:

\(
\beta_t^{(n-1)’} = Cov_t \left( rx_{t+1}^{(n-1)}, v_{t+1}’ \right) \Sigma^{-1}
\)

por lo que la anterior ecuación se simplifica

\(
E_t \left[ rx_{t+1}^{(n-1)} \right] = \beta_t^{(n-1)’} \left( \lambda_0 + \lambda_1 X_t \right) – \frac{1}{2} Var_t \left( rx_{t+1}^{(n-1)} \right)
\)

Esto, a su vez, se utiliza para descomponer el exceso de rentabilidad en un componente correlacionado con \(v_{t+1}\) y otro que es condicionalmente ortogonal

\( rx_{t+1}^{(n-1)} – E_t^{\mathbb{P}} \left[ rx_{t+1}^{(n-1)} \right] = \beta_t^{(n-1)’} v_{t+1} + \varepsilon_{t+1}^{(n-1)} \)

\( \varepsilon_{t+1}^{(n-1)} \sim iid\, N(0, \sigma^2) \)

Asimismo, se desagrega los retornos en exceso en los siguientes componentes

\( rx_{t+1}^{(n-1)} = \beta_t^{(n-1)’}(\lambda_0 + \lambda_1 X_t) – \frac{1}{2} \left( \beta_t^{(n-1)’} \Sigma \beta_t^{(n-1)’} + \sigma^2 \right) + \beta_t^{(n-1)’} v_{t+1} + \varepsilon_{t+1}^{(n-1)} \)

En términos financieros esto implica las siguientes fuentes de retornos en exceso

Retorno en exceso = Retorno esperado + Convexidad + Choque de factores de riesgo+ Residuo

Finalmente agregando las tasas para todos los \(N\) vencimientos y \(T\) periodos, entonces

\(
rx = \beta'(\lambda_0 \mathbf{1}_T’ + \lambda_1 X_-) – \frac{1}{2} \left( B^* \, {vec}(\Sigma) + \sigma^2 \mathbf{1}_N \right) \mathbf{1}_T’ + \beta’ V + E
\)

Donde \(rx\) representa la matriz de exceso de retornos de dimensión \(N \times T\), \(\beta = \left[ \beta^{(1)} \ \beta^{(2)} \ \dots \ \beta^{(N)} \right]\) es una matriz de sensibilidades de \(K \times N\). Asimismo, \(\mathbf{1}_T\) y \(\mathbf{1}_N\) son vectores de unos de dimensiones \(T \times 1\) y \(N \times 1\), respectivamente. La matriz de factores rezagados \(X_- = \left[ X_0 \ X_1 \ \dots \ X_{T-1} \right]\) de \(K \times T\), \(B^* = \left[ {vec}(\beta^{(1)} \beta^{(1)’}) \ {vec}(\beta^{(2)} \beta^{(2)’}) \ \dots \ {vec}(\beta^{(N)} \beta^{(N)’}) \right]’\) es una matriz de \(N \times K^2\), \(V\) es una matriz de \(K \times T\) y \(E\) es la matriz de errores de \(N \times T\).

Estimación del modelo

Para estimar las ecuaciones especificadas anteriormente, se realizan las siguientes etapas

Etapa I: Se utiliza PCA para obtener el vector de factores de riesgo \(X_t\) y luego estimamos un \(VAR(1)\) para obtener \(\hat{\mu}\), \(\hat{\Phi}\), \(\hat{V}\) y la matriz de varianzas y covarianzas \(\hat{\Sigma} = \frac{1}{T} \hat{V} \hat{V}^{\prime}\)

Etapa II: Mediante el uso de MCO se estima la ecuación de retornos en exceso

\(
rx = a \mathbf{1}_T^{\prime} + \beta^{\prime} \hat{V} + c X_{t} + E
\)

obtenemos loscoeficientes \(\hat{a}\), \(\hat{\beta}\), \(\hat{c}\) y \(\hat{\sigma}^2\). Finalmente, se construye \(\hat{B}^{*}\) a partir de \(\hat{\beta}\).

Etapa III: Se obtiene el market price of risk apartir de las siguientes ecuaciones

\( \hat{\lambda}_0 = \left( \hat{\beta} \hat{\beta}^{\prime} \right)^{-1} \hat{\beta} \left( \hat{a} + \frac{1}{2} \left( \hat{B}^{*} \, \mathrm{vec}(\hat{\Sigma}) + \hat{\sigma}^2 \mathbf{1}_N \right) \right) \)

\( \hat{\lambda}_1 = \left( \hat{\beta} \hat{\beta}^{\prime} \right)^{-1} \hat{\beta} \hat{c} \)

Etapa IV: Se utiliza MCO para para estimar la ecuación de la tasa corta para obtener \(\hat{\delta}_0\) y \(\hat{\delta}_1^{\prime}\)

\( \begin{aligned} r_t &= \delta_0 + \delta_1^{\prime} X_t + e_t \\ e_t &\sim iid\, N(0, \sigma_e^2) \end{aligned} \)

Etapa V: Usando los coeficientes estimados anteriormente, a continuación, se construye la curva de rendimientos riesgo neutral y las primas a plazo.

Curva de Rendimientos

Para un bono cupón cero con vencimiento a \(n\) periodos, se estima su precio en \(t\) mediante la siguiente forma

\( \hat{P}_t^{(n)} = e^{\hat{A}_n + \hat{B}_n^{\prime} X_t} \)

Asimismo, existe una relación inversa entre el precio del bono y su tasa de rendimiento

\( \hat{P}_t^{(n)} = e^{-\hat{y}_t^{(n)}} \times (n) \)

A partir de las dos ecuaciones anteriores despejamos las tasas estimadas

\( \hat{y}_t^{(n)} = \frac{-1}{n} \ln\left( \hat{A}_n + \hat{B}_n^{\prime} X_t \right) \)

Donde

\( \hat{A}_n = \hat{A}_{n-1} + \hat{B}_{n-1}^{\prime} (\hat{\mu} – \hat{\lambda}_0) + \frac{1}{2} \left( \hat{B}_{n-1}^{\prime} \hat{\Sigma} \hat{B}_{n-1} + \hat{\sigma}^2 \right) – \hat{\delta}_0 \)

\( \hat{B}_n^{\prime} = \hat{B}_{n-1}^{\prime} \left( \hat{\Phi} – \hat{\lambda}_1 \right) – \hat{\delta}_1^{\prime} \)

Establecemos como valores iniciales: \(\hat{A}_0 = \hat{B}_0^{\prime} = 0\)

Curva de expectativas riesgo neutral:

Según CEMLA (s.f.), una forma general de interpretar el promedio de expectativas de la tasa de corto plazo es considerarlo como la tasa de largo plazo que prevalecería si el agente fuera neutral al riesgo. En consecuencia, las tasas de largo plazo neutrales al riesgo permiten aislar e identificar la prima por plazo.

Sea el promedio de las tasas de corto plazo esperado para los próximos \(n\) periodos

\( Exp_t^{(n)} = \frac{1}{n} \sum_{i=0}^{n-1} E_t(r_{t+i}) \)

Establecemos \(\hat{\lambda}_0 = \hat{\lambda}_1 = 0\) para introducir un entorno riesgo neutral

\( Exp_t^{(n)} = \frac{-1}{n} \ln\left( \tilde{A}_n + \tilde{B}_n^{\prime} X_t \right) \)

Donde

\( \tilde{A}_n = \tilde{A}_{n-1} + \tilde{B}_{n-1}^{\prime} (\hat{\mu}) + \frac{1}{2} \left( \tilde{B}_{n-1}^{\prime} \hat{\Sigma} \tilde{B}_{n-1} \right) – \hat{\delta}_0 \)

\( \tilde{B}_n^{\prime} = \tilde{B}_{n-1}^{\prime} (\hat{\Phi}) – \hat{\delta}_1^{\prime} \)

Establecemos como valores iniciales: \(\tilde{A}_0 = \tilde{B}_0^{\prime} = 0\)

Finalmente dado que la prima plazo \(TP_t^{(n)}\) refleja la compensación que exige el tenedor de un bono nominal con vencimiento a \(n\) periodos por por asumir riesgos macrofinancieros asociados a su horizonte de inversión, esta puede estimarse como el residuo que resulta de descontar el promedio de las tasas implícitas de corto plazo esperadas de la curva de rendimientos estimada

\( TP_t^{(n)} = \hat{y}_t^{(n)} – Exp_t^{(n)} \)

Asimismo, es posible identificar en cada periodo \(t\) cada componente de cualquier tasa observada con vencimiento a \(n\) periodos en la curva de rendimientos

\( y_t^{(n)} = TP_t^{(n)} + Exp_t^{(n)} + u_t^{(n)} \)

Donde \(u_t^{(n)}\) representa el error del modelo

Determinantes de la prima a plazo

Una vez estimada la serie de la prima a plazo \(Y_t\), la pregunta que buscamos responder es ¿Cuáles son los factores macrofinancieros que determinan la prima a plazo para cada país de LATAM?

Siguiendo la metodología de Aguilar-Argaez et al. (2020), se utiliza un modelo con coeficientes cambiantes en el tiempo (TVP) para capturar las relaciones dinámicas entre la prima por plazo local y sus determinantes externos y domésticos. El uso de un modelo TVP se fundamenta en que las relaciones entre la prima por plazo y sus determinantes no son constantes a lo largo del tiempo, sino que se ven afectadas por cambios en el entorno macroeconómico doméstico, episodios de estrés financiero y choques de incertidumbre externa.

Sea el vector de coeficientes cambiantes en el tiempo \(\beta_t = \left[ \beta_t^{(US)},\, \beta_t^{(D)},\, \beta_t^{(Vol)} \right]^{\prime}\) y las variables \(X_t = \left[ TP_t^{(US)},\, D_t,\, Vol_t \right]\). Donde \(TP_t^{(US)}\) denota la prima a plazo de Estados Unidos, \(D_t\) denota el déficit fiscal (como % del PIB) de un país de LATAM y \(Vol_t\) la volatilidad estocástica del tipo de cambio correspondiente a dicha economía (ver recuadro del FlarBlog: “América Latina en 2024: Estabilidad macroeconómica en un contexto global mixto y cambiante). Podemos representar el modelo en su forma Estado – Espacio Gaussiano.

Ecuación de Medida

\( \begin{aligned} Y_t &= X_t \beta_t + u_t \\ u_t &\sim iid\, N\left(0, \sigma_u^2\right) \end{aligned} \)

Donde \(u_t\) representa el error de medida.

Ecuación de Estado

\(
\begin{aligned}
\beta_t &= F\beta_{t-1} + \nu_t \\
\nu_t &\sim iid\, N\left(0, \sigma^2_\nu\right) \\
\operatorname{cov}(u_t, \nu_t) &= 0
\end{aligned}
\)

Donde \(\nu_t\) representa el error de estado.

Además, los errores son independientes \(\operatorname{cov}(u_t, \nu_t) = 0\)

Finalmente, para estimar este sistema de ecuaciones utilizamos el Filtro de Kalman.

Los datos

Este estudio estima la prima a plazo con datos diarios de la curva de rendimientos de Estados Unidos, Brasil, Chile, Colombia, México y Perú entre abril de 2008 y mayo de 2025. Para analizar sus determinantes, se utilizan datos mensuales, promediando la prima a plazo por mes, en línea con la frecuencia de las variables macroeconómicas consideradas.

Referencias

Ceballos, L., Naudon, A., & Romero, D. (2015, febrero). Nominal term structure and term premia: Evidence from Chile (Documento de Trabajo N.° 752). Banco Central de Chile.

Lutz, F.A. 1940. The structure of interest rates, the quarterly journal of economics.

Dai, Q. and Singleton, K. J. (2000). Specification Analysis of A_ne Term Structure Models. Journal of Finance, 55(5):1943_1978.

Joslin, S., Singleton, K. J., and Zhu, H. (2011). A New Perspective on Gaussian Dynamic Term Structure Models. Review of Financial Studies, 24(3):926-970.

Duffee, G. (2002). Term Premia and Interest Rate Forecasts in Affine Models. Journal of Finance, 57:405-433.

Campbell, J. Y., & Shiller, R. J. (1991). Yield Spreads and Interest Rate Movements: A Bird’s Eye View. The Review of Economic Studies, 58(3), 495-514.

Adrian, T., Crump, R. K., & Moench, E. (2013). Pricing the Term Structure with Linear Regressions. Journal of Financial Economics, 110(1), 110-138.

Litterman, R. B. and Scheinkman, J. (1991). Common Factors Afecting Bond Returns. Journal of Fixed Income, 1(1):54-61.

Fama, Eugene and Bliss, Robert R., 1987, The Information in Long-Maturity Forward Rates, American Economic Review, 1987, vol. 77, issue 4, 680 – 92.

Cochrane, John, H., and Monika Piazzesi. 2005. Bond Risk Premia. American Economic Review 95 (1): 138–160.

Dybvig, P. H., and S. A. Ross. (1987). Arbitrage. In J. Eatwell, M. Milgate and P. Newman (eds.), The New Palgrave: A Dictionary of Economics. Palgrave Macmillan, pp.100-106.

Centro de Estudios Monetarios Latinoamericanos. (s.f.). Term premium estimates. Recuperado el 5 de julio de 2025, de https://www.cemla.org/DatosSelectosMacroeconomicos/Term%20premium%20estimates%20eng.html#estimates

Muth, J. F. (1961). Rational Expectations and the Theory of Price Movements. Econometrica, 29(3), 315-335.

Diebold, F. X., & Li, C. (2006). Forecasting the term structure of government bond yields. Journal of Econometrics, 130(2), 337–364.

Diebold, F. X., Rudebusch, G. D., & Aruoba, S. B. (2004). The Macroeconomy and the Yield Curve: A Dynamic Latent Factor Approach. (FRBSF Working Paper 2003 18). Federal Reserve Bank of San Francisco.

Svensson, L. E. O. (1995). Estimating Forward Interest Rates with the Extended Nelson & Siegel Method. Sveriges Riksbank Quarterly Review, 3(1):13-26.

Cook, T, and Hahn, T 1990. Interest Rate Expectations and the Slope of the Money Market Yield Curve. Federal Reserve Bank of Richmond Economic Review 76(5): 3–26.

Vasicek, O. (1977). An Equilibrium Characterization of the Term Structure. Journal of Financial Economics, 5(2):177-188.

Aguilar-Argaez, A., Diego-Fernández, M., Elizondo, R., & Roldán-Peña, J. (2020). Dinámica de la prima por plazo y sus determinantes: El caso mexicano. Documento de investigación No. 2020-18, Banco de México.